平动、转动、定轴转动、定点运动、自转、公转
最近更新:2024.8.23
描述刚体的运动,需要平动、定轴转动、定点运动等名词;描述参考系的运动,需要平动、定轴转动等名词;描述质点的运动,前述几个名词本来是用不上的;天文学习惯于使用公转和自转两个词。
物理教学中,转动一词的用法比较复杂。通常把转动作为定轴转动的同义词;有人把质点的圆周运动、物体质心的圆周远动也称为转动;有人把质点的椭圆运动也称为转动;有人把定点运动称为定点转动,把转动作为定轴转动和定点转动的总称。后两种用法,尤其有害。
公转也不止一种用法。在“地球绕太阳公转”这样的语境,公转是指地心在日心参考系中做椭圆运动(非常接近于圆周),不是平动、不是定轴转动、不是定点运动,与描述刚体运动的那些概念无关。在“地球绕太阳的运动是自转和公转的叠加”这样的语境,地球公转是指地球的一种平动,平动地球的每一点的轨迹为椭圆(非常接近于圆周)。后一种用法少见。
平动
一个人带着头盔,沿楼梯上下左右走动,如果头盔上每条轮廓线的方向都不变,那么头盔的运动就是平动。
平动具有下列性质:
每条轮廓线的位置随时间变化,而方向不变; 不同点的轨迹形状相同; 不同点的速度相同; 不同点的加速度相同。给平动下定义,只要列出上述性质中一条、两条就行了。
上述平动着的钢盔上的每一点的运动轨迹,不是直线、不是平面曲线,而是空间曲线。物理教材主要讨论简单的例子,每一点的轨迹都是平面曲线。
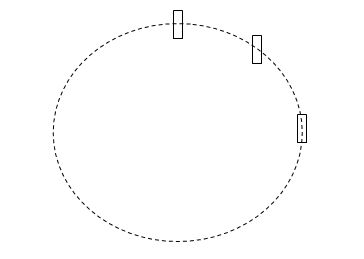
图1. 长方体平动。
图1中,长方形(长方体)做平动,质心,以及每个点的运动轨迹都是椭圆。这个图还可以改得更特殊一点:质心以及每个点的运动轨迹都是圆周。
定轴转动
简单地说,刚体上有一条线保持不动,而其余的点都做圆周运动,就是定轴转动。准确地说,在所选参考系中,刚体或其“延长体”上如果有一条线保持不动,其他点都做圆周运动,那么,这条线称为转动轴,这个运动称为定轴转动。
定轴转动具有下列性质:
轴外各点的运动轨迹都是圆周、圆弧。所有圆周的圆心都在一条直线上,也就是转动轴上。 轴外各点的角速度都一样; 轴外各点的角加速度都一样; 轴外各点的加速度不都一样,离轴较近的加速度较小; 有些轮廓线的方向随时间变化,有些不变。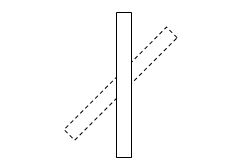
图2. 长方体定轴转动。
图2中,长方体在两个时刻的位置分别用实线和虚线表示,垂直于纸面过长方体中心的那条线的位置不随时间变化,这个运动是定轴转动。这个转动轴经过刚体的质心;一般地,转动轴可以不经过刚体的质心。
像图2这样,转动轴过图中一点垂直于纸面,读者看不到作为转动轴的一条线,看到的是一个点。绕某直线转动常常表述为绕某点转动。“绕某点转动”只是一个通俗化的表述,多采用严格的表述为好。即使物体是薄片,厚度为零,也是使用严格表述为好。
惯性系中的定轴转动跟非惯性系中的定轴转动满足的力矩等式不同。汽车停着、匀速行驶,汽车主体可看做惯性系,对相对车体定轴转动的车门,不需要考虑惯性力力矩。汽车变速行驶、转弯、翻跟头,汽车主体不可看做惯性系,对相对车体定轴转动的车门,需要考虑惯性力力矩。
定点运动
刚体或其“延长体”上,如果只有一个点保持不动,其他点都运动,那么,不动的点称为定点,刚体的这种运动称为定点运动。定点运动的刚体上,任一点的位置与定点的距离保持不变,但轨迹不是圆周、圆弧。
定点运动比定轴转动复杂得多。对定轴转动,可以用角速度统一描述各点运动的一个方面;对定点运动,虽然也使用角速度,但这个角速度是相对于“瞬轴”(“瞬时转动轴”),相邻时刻的瞬轴总是不同。
刚体的任意运动
平动 定轴转动 定点运动 平动和平动的叠加 平动和定轴转动的叠加 平动和定点运动的叠加 刚体的其他运动平动和定轴转动的叠加
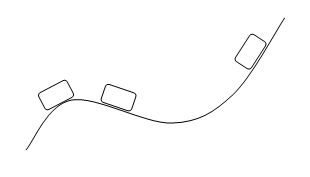
图3:长方形(长方体)沿着曲面滑动。
图3中长方形的运动,是一个平动和一个定轴转动的叠加。转动轴经过质心垂直于纸面。这个定轴转动,不是周期性运动,谈不上周期,但它和周期性的定轴转动一样,服从定轴转动动力学方程。
其定轴转动的角速度是变化的,外力对于转动轴的力矩不是保持为零,外力的作用线不是交于一点。
上面把图3长方体作为刚体处理, 同时考虑平动和定轴转动,只做了定性的描述。要沿着这个思路定量计算,十分困难,所以大学物理不作为平动与定轴转动叠加的范例来介绍。(圆柱体在曲面上作无滑滚动,作为平动叠加定轴转动的范例来介绍比较方便。)中学物理把图3所示的长方体作为质点,也就不谈它的定轴转动。
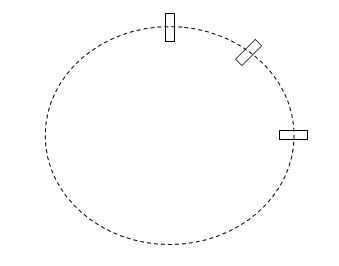
图4. 平动叠加定轴转动。
图4中,长方体的运动是图1所示的平动与图2所示的定轴转动的叠加,其平动与定轴转动的“方向”相同(都是顺时针,或者都是逆时针),周期相等。
把图4中的椭圆改为圆周,那么,长方体的运动仍然可以表述为平动与定轴转动的叠加,也可以表述为一个单纯的定轴转动(转动轴是经过这个图的中心点垂直于纸面的直线)。
图3和图4两个例子,质心的运动轨迹在一平面上,转动轴跟质心运动轨迹平面垂直。这样的运动称为平面平行运动。做平面平行运动的刚体,每一点的轨迹都在一个平面,各平面彼此平行。平动和定轴转动的叠加,有的是平面平行运动,有的不是。
自转和公转
天体物理常用的参考系是日心参考系、地心参考系、月心参考系等[1]。这些参考系原点分别位于日心、地心、月心,坐标轴都是指向其他星系中心或遥远恒星。“遥远恒星”是指比太阳更遥远的恒星。这些参考系彼此相对平动。
在地心参考系中,地球绕地轴做定轴转动,天体物理、天文学把天体的这种定轴转动称为自转。
在地心参考系中,月球差不多始终以同一面(半个球面)面对地球,类似于图4中长方体的一个面始终朝着椭圆的中心。月球的运动是图1所示的平动与图2所示的转动的叠加,平动和转动的周期正好相同,“运动方向”相同。图1所示的平动可以称为公转,这是公转的含义之一。月球自转轴跟月心运动轨迹所在平面的夹角是87.46度,接近垂直。如果严格垂直,且那个椭圆是圆,那么前文中的“差不多”可以去掉。
一般地,行星中心参考系中卫星的运动、恒星中心参考系中行星的运动、星系中心参考系中恒星的运动,都是公转叠加自转。这种语境下,公转都是指平动[2],每个点的轨迹都是椭圆,文献[3]有关说法是不对的。
地球的运动
在日心参考系,地球绕太阳公转同时自转,公转周期是365日6时9分10秒(恒星年),自转周期是23时56分4秒(恒星日)。地球自转轴跟地心运动轨迹所在平面的夹角66度多一点。“地球自转方向与公转方向相同”只是一种粗糙的说法,通俗的说法。 在地心参考系,地球的运动是转动,是自转,自转周期也是23时56分4秒。 在原点位于日心,两个坐标轴指向两个遥远恒星,一个坐标轴指向地心,这样一个参考系,地球的运动是转动,是自转,平均周期为24小时(太阳日)。日、天是太阳日的简称,等于24小时。 在原点位于地心,两个坐标轴指向两个遥远恒星,一个坐标轴指向日心,这样一个参考系,地球的运动是转动,是自转,平均周期也是24小时。月球的运动
在地心参考系,月球绕地球公转同时自转,公转周期是27.32 天,自转周期也是27.32天。月球自转轴跟月心运动轨迹所在平面成87.46度。 在原点位于地心,两个坐标轴指向两个遥远恒星,一个坐标轴指向太阳中心,这样一个参考系,月球作公转和自转,公转周期约为29.53天,自转周期也是29.53天。月相周期决定于这个参考系中月球的公转周期,也是29.53天。假如月球自转周期不是现在这个值,而公转周期仍是现在这个值,那么,月相周期就仍是现在这个值。农历月的平均长短,29.53天(朔望月),是根据月相周期确定的。参考文献
[1]吴建国,参考系、参照物 https://www.risechina.org/3645
[2]梁昆淼. 力学.上册.2版[M]. 人民教育出版社(高等教育出版社), 1978:309.
“取地球中心为基点研究月球的运动,整个月球随着月心绕地球运行,这就是月球的公转(一种平动!)。与此同时,月球任一指定的半径在空间中的指向也在改变,这就是月球的自转。”(感叹号是原文就有的。取地球中心为基点,就是本文所说的采用地心参考系。)
[3]陈文德. 地球平动问题研究[J]. 福建教育学院学报, 2002(7):2.
该文不同意“公转是一种平动”,理由是,卫星、行星上一般的线段在空间中的方向会随时间变化。这个理由是无效的。采用“公转是一种平动”说法的人们并没有说天体只做公转。卫星、行星上的一般线段的方向随时间的变化,是自转这个概念所蕴含的。文中这样一句话“天文界及有关刊物编审也认为公转必定是平动”,倒是令人欣慰。
相关博文: 评失重和超重概念评“重力是引力的一个分力”评楞次定律的几种表述引力·重力·失重飞船沿着什么路线从地球飞向月球?7,784
相关知识
Cybex Eagle NX 躯干式转动训练器
幼儿园大班健康(体育)活动:《呼啦圈转转转》
什么是运动疗法 (转载)
有氧运动转氨酶会升高吗
[转载]下蹲运动有益健康
运动是转换心情的钥匙
新闻观察:运动康复兴起:公众健康从“爱运动”转向“会运动”
运动才能使你健康(转)
大班健康公开课教案及教学反思《呼啦圈转转转》
高强度运动,能使高转移性癌症发病率降低73%!哪些运动可以做?
网址: 平动、转动、定轴转动、定点运动、自转、公转 https://m.trfsz.com/newsview683844.html