双自旋机构

双自旋机构（Dual Spin Device）是一种姿态控制系统，其基本构成为一个刚体航天器和一个镶嵌其中的飞轮。飞轮可绕某物体坐标系中的固定轴旋转以改变整体的角动量分配，从而改变航天器其余部分的角动量。

结构与运动方程

双自旋机构的基本结构如下所示。

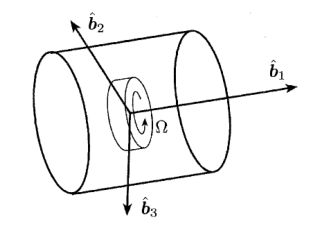
一个视为刚体的航天器（不一定具有对称性）内部镶嵌有飞轮，飞轮转轴固联在ˆb1^b1上。航天器（不含飞轮）的惯量张量为[Is][Is]，角速度为ˆω^ω。飞轮惯量张量为[Iw][Iw]，绕转轴的转动惯量为IwIw，相对于航天器的角速度大小为ΩΩ（按右手螺旋定则确定正负）。则，整个系统的惯量张量[I][I]和角动量ˆH^H可表示为：

[I]=[Is]+[Iw][I]=[Is]+[Iw] ˆH=[I]ˆω+IwΩˆb1^H=[I]^ω+IwΩ^b1

根据角动量定理： ˙H=ˆL˙H=^L 且利用角速度的性质，对角动量求导有： ˙H=Nd[I]ˆωdt+Nd(IwΩˆb1)dt=Bd[I]ˆωdt+ˆω×[I]ˆω+Bd(IwΩˆb1)dt+ˆω×(IwΩˆb1)=[I]˙ω+[˜ω][I]ˆω+Bd(IwΩ)dtˆb1+IwΩˆω׈b1 令h=IwΩ，h为一个标量，且与参考系无关。有： ˙H=[I]˙ω+[˜ω][I]ˆω+˙hˆb1+hˆω׈b1=[I]˙ω+[˜ω][I]ˆω+˙hˆb1+hω3ˆb2−hω2ˆb3 在无力矩运动的情况下，ˆL=0，因此： [I]˙ω=−[˜ω][I]ˆω−˙hˆb1−hω3ˆb2+hω2ˆb3 即为双自旋机构的旋转方程。展开，有： [I1000I2000I3][˙ω1˙ω2˙ω3]=−[(I3−I2)ω2ω3(I1−I3)ω1ω3(I2−I1)ω1ω2]+IW[−˙Ω−Ωω3Ωω2] 写成标量形式： {˙ω1=I2−I3I1ω2ω3−IWI1˙Ω˙ω2=I3−I1I2ω1ω3−IWI2ω3Ω˙ω3=I1−I2I3ω1ω2−IWI3ω2Ω

稳定性分析

根据极迹图，若刚体围绕转动惯量次大的轴旋转，会出现不稳定现象。双自旋机构克服了这一点。

此处的“稳定”指的是长时间角速度维持不变。设稳定时角速度为ˆωe，则˙ωe=0。在飞轮满足特定转速条件时，双自选机构能实现航天器绕着ˆb1轴旋转的任意角速度下的稳定，航天器绕b1轴的转动惯量无特别要求。

设平衡状态下飞轮相对角速度不变，即： ˙Ω=0

设角速度有一小扰动： ˆω=ˆωe+δˆω 平衡状态： {˙ωe1=I2−I3I1ωe2ωe3=0˙ωe2=I3−I1I2ωe1ωe3−IwI2ωe3Ω=0˙ωe3=I1−I2I3ωe1ωe2+IwI3ωe2Ω=0 将ˆω代入，并忽略二次及以上高阶项。注意到航天器绕着ˆb1轴旋转，有ωe2=ωe3=0。代入化简，有： {δ˙ω1=0δ˙ω2=I3−I1I2ωe1δω3−IwI2δω3Ωδ˙ω3=I1−I2I3ωe1δω2+IwI3δω2Ω 由后两式，可写出关于ωe2的独立的微分方程： δ¨ω2+(I1−I3I2ωe1+IwI2Ω)(I1−I2I3ωe1+IwI3Ω)δω2=0 类比于弹簧-振子系统，在一次项系数为正时，系统稳定。令ˉΩ=Ωωe1，有： ω2e1I2I3(I1−I3+IwˉΩ)(I1−I2+IwˉΩ)>0 可用Ω=0的情况进行验证。此时双自旋机构退化为一般刚体，上式要求： {I1>I3I1>I2,or{I1<I3I1<I2 即ˆb1轴所对应转动惯量在三轴中为最大或最小。这与极迹图的结论相符。 对于一般情况，有要求： {I1>I3−IwˉΩI1>I2−IwˉΩ,or{I1<I3−IwˉΩI1<I2−IwˉΩ 可以依据不等式进行相对角速度ˉΩ的正负性判断。最终的判断结果如下所示。

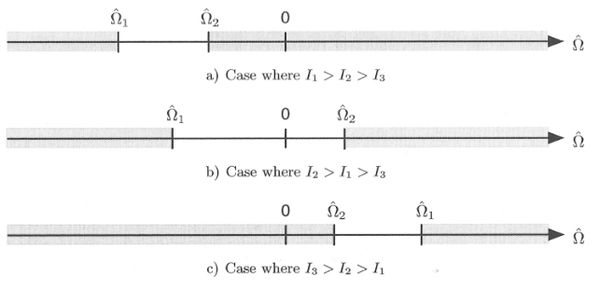
消旋研究

以下为一回稳过程的经典案例。

假设飞轮初始相对航天器静止。航天器围绕ˆb2或ˆb3轴做旋转运动。飞轮逐渐转动，直到其角动量大小与初始航天器的角动量大小相同。

对整个体系，合外力矩为零，有： H=|ˆH(t0)| 飞轮的角动量随时间线性增长，有： ˙h=Iw˙Ω 因此，总的机动时间为： Tmax=HIw˙Ω 理想状态下，飞轮占有了航天器所有的角动量，而体系角动量守恒，因此航天器剩余部分角动量为零，航天器实现消旋。然而，因为该过程只控制了角动量的大小，而没有控制方向，因此矢量相减下航天器剩余部分仍有角动量，不能彻底消旋。情景如下图所示。

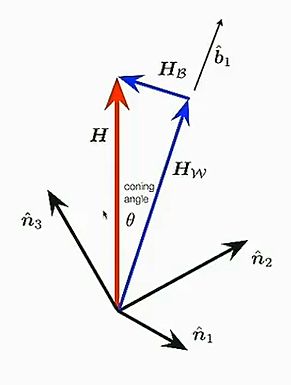
其中ˆHw为飞轮角动量，而ˆHB为消旋后航天器剩余部分的角动量。θ被称为“圆锥角”（Coning Angle）。在圆锥角为零时ˆHB=0，而θ=0并不能被保证。

通过模拟可发现，当机动时间越长，即飞轮加速越缓慢时，圆锥角就越小，消旋也就越彻底。下图即显示了仿真结果。[1]蓝色曲线为200秒机动下的圆锥角变化，红色为1000秒下的。

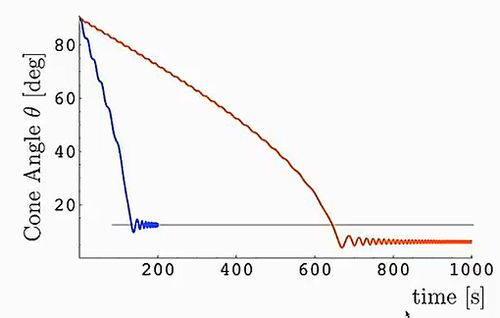
极迹图研究

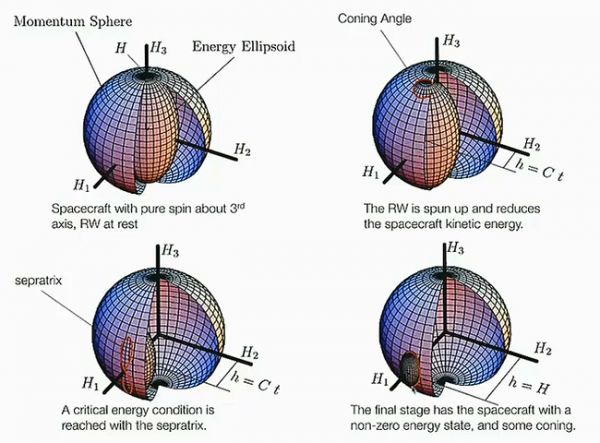
圆锥角的出现可用极迹图来解释。整个消旋过程中，航天器非飞轮部分的能量为： E=12(I1ω21+I2ω22+I3ω23) 整体的角动量有： H2=H21+H22+H23 角动量守恒，在物体坐标系中大小不变。因此有角动量球。

另有能量椭球： (H1−h)22I1E+H222I2E+H232I3E=1 两者交线即为角动量矢量能移动范围。而整个消旋过程中，能量椭球一直在变化（如下图所示[1]）

评价

双自旋机构实现了一般刚体不能实现的绕任意轴达到稳定的要求，也在不要求调整时间的情况下具有较好的消旋特性，因此常作为航天器动量交换机构的理论基础。反作用轮即是在其基础上改进而得出的。

姿态力学

已有词条

姿态力学|坐标系|刚体|质心|右手定则

方向余弦矩阵|欧拉角|主旋转矢量|欧拉四元数|吉布斯矢量|经典罗德里格斯参数|修正罗德里格斯参数

俯仰角|滚转角|偏航角|欧拉角序列3-2-1

欧拉角序列1-2-1|欧拉角序列1-2-3|欧拉角序列1-3-1|欧拉角序列1-3-2|欧拉角序列2-1-2|欧拉角序列2-1-3|欧拉角序列2-3-1|欧拉角序列2-3-2|欧拉角序列3-1-2|欧拉角序列3-1-3|欧拉角序列3-2-3

角速度|凯莱变换|奇点|万向节锁

欧拉方程

转动惯量|角动量|动能|进动|章动|无力矩运动

动量交换机构|重力梯度|潮汐锁定|极迹图

李雅普诺夫稳定|饱和|未知干扰力矩|增益选择

双自旋机构|刚体消旋问题|刚体定姿消旋问题|磁控制|悠悠球消旋

刚体追踪问题|刚体定姿追踪问题

TRIAD方法|Q方法